奉贤中学2018-2019学年度2019届9月份开学考试数学试题
1、填空题。
1.设集合
集合
，若
,则
_______.
2.
_________.
3.抛物线的焦点为椭圆
的右焦点,顶点在椭圆的中心,则此物物的规范方程为___________.
4.二项式
的展开式中的常数项为_________.
5.在△ABC中,角A、B、C的对边分别为
,若
,则∠C=______.
6.已知圆锥的全方位积是底面积的3倍,那样该圆锥的侧面展开图扇形的圆心角为________.
7.把函数
的图像上所有些点的横坐标缩短到原来的倍,再把所得图像上所有点向左平行移动
个单位长度,得到的图像所表示的函数分析式为__________.
8.若
,且
的最小值为9,则
__________.
9.在随机抽取的9位同学中,至少有2位同学在同1月份生的概率为__________
10.在由正整数构成的无穷数列
中,对任意
,都有
,且对任意的
，数列中怡有
个,则
_________.
11.已知P为双曲线
上的点,点M满足
,且
,则当获得最小值时的点P到双曲线C的渐近线的距离为________.
12.对于概念在R上的函数
,有下述命题:
①若是奇函数,则的图像关于点A对称；
②若函数的图像关于直线
对称,则为偶函数；
③若对,有,则2是的一个周期；
④函数与
的图像关于直线对称.
其中正确的命题是____________.
2、选择题。
13.空间两条直线
与直线
都成异面直线,则的地方关系是
A.平行或相交 B.异面或平行 C.异面或相交 D.平行或异面或相交
14.奇函数在区间
上为减函数,且有最小值2,则它在区间
上
A.是减函数，有最大值-2 B.是增函数，有最大值-2
C.是减函数，有最小值-2 D.是增函数，有最小值-2
15.函数
与
在同一坐标系的图像又公共点的充要条件是
A.
B.
C.
D.
16.数列满足,且对于任意的,都有
,则
A. B.
C.
D.
3、解答卷。
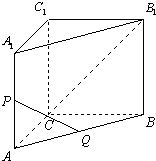
17.如图,在直三棱柱中,=AC=BC=2,∠ACB=90°,P是
中点,Q是AB的中点.
求证:PQ⊥平面
；
求直线与平面PCQ所成角的大小.
18.已知函数的最小正周明为π.
求
的值；
求函数在区间在上的取值范围。
19.已知数列中,
.
证明数列是等比数列,并求数列的通项公式；
在数列中,是不是存在连续三项成等差数列?若存在,求出所有符合条件的项；若没有,请说明理由。
20.已知涵数
且满足.
求实数的值；
判断函数在区间
上的单调性,并用单调性的概念证明；
若关于的方程和有三个不一样的实数解,求实数的取值范围。
21.已知圆C过定点A,圆心C在抛物线
上,M、N为圆C与轴的交点.
求圆C半径的最小值；
当圆心C在抛物线上,
是不是为肯定值?请证明你的结论；
当圆心C在抛物线上运动时,记
求的最大值,并求此时圆的方程。
